Heap is a special Tree based Data-Structure in which the tree is a complete binary tree.
It is generally of two types -
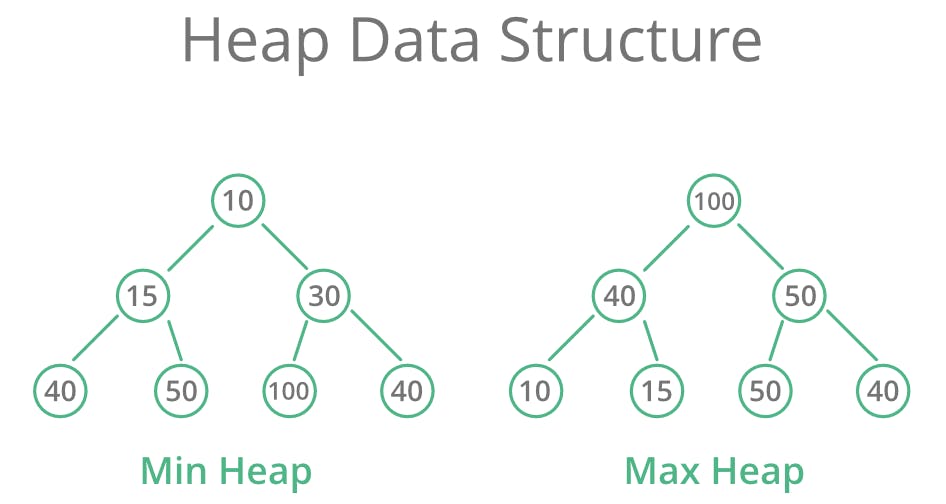
Max-heap - where the root node must be greatest among all its child nodes and the same goes for its right subtree and left subtree.
Min-heap - where the root node must be smallest among all its child nodes and the same goes for its right subtree and left subtree.
Operations on a Heap -
insert() - Inserts data into Heap.
extract min() - Extracts and deletes the smallest element in the Heap while maintaining its properties.
decreaseKey() - Changes an element at an index in the Heap while maintaining its properties.
deleteKey() - Deletes an element at an index in the Heap while maintaining its properties.
heapify() - The process of creating a heap data structure from a binary tree represented using an array.
buildHeap() - converts an array into a Heap using the help of heapify function.
getMin()/getMax() - Returns the minimum/maximum element of the Heap.
Implementation of Heap -
Heap is represented using arrays where the element at the 0-th index is greatest in the case of a Max-heap and minimum in the case of a Min-heap.
We find the right and left child using the formula -
left child = 2*i+1
right child = 2*i+2
parent = (i-1)/2
Here, i is the index of the node.
#include <iostream>
using namespace std;
class Heap
{
int size;
int capacity;
int arr[];
Heap(int c)
{
size = 0;
capacity = c;
arr = new int[c];
}
int leftChild(int i) // extracts left child Index
{
return (2 * i + 1);
}
int rightChild(int i) // extracts right child index
{
return (2 * i + 2);
}
int parent(int i) // extracts parent index of a node
{
return (i - 1) / 2;
}
insert(int x) // Time Complexity o(logn) // inserts in Heap
{
if (size == capacity)
return;
size++;
arr[size - 1] = x;
int i = size - 1;
while (i != 0 && arr[parent(i)] > arr[i])
{
swap(arr[parent(i)], arr[i]);
i = parent(i);
}
}
void minHeapify(int i) { // Time Complexity O(logN)
int li = leftChild(i), ri = rightChild(i);
int smallest = i;
if (li < size && arr[li] < arr[smallest])
{
smallest = li;
}
if (ri < size && arr[ri] < arr[smallest])
{
smallest = ri;
}
if (smallest != i)
{
swap(arr[i], arr[smallest]);
minHeapify(smallest);
}
}
int getMin() // extracts minimum element from heap
{
return arr[0];
}
int extractMin()//removes minimum element from heap and returns it
{
if (size == 0)
return INT_MAX;
if (size == 1)
{
size--;
return arr[0];
}
swap(arr[0], arr[size - 1]);
size--;
minHeapify(0);
return arr[size];
}
void decreaseKey(int i, int x) //changes a heap element at index i
{
arr[i] = x;
while (i != 0 && arr[parent(i)] > arr[i])
{
swap(arr[parent(i)], arr[i]);
i = parent(i);
}
}
void deleteKey(int i) // deletes a element at i index
{
decreaseKey(i, INT_MIN);
extractMin();
}
void buildHeap() // T.C. O(N) //builds the heap using heapify()
{
for (int i = (size - 2) / 2; i >= 0; i--)
{
minHeapify(i);
}
}
}
Applications of Heap -
Heap is used to constructing a priority_queue
Heap sort is the fastest sorting algorithm with time complexity O(N*logN) and is easy to implement.
priority_queue -
In c++, the STL priority_queue provides the functionality of the priority queue which is internally created using Heap Data-Structure.
To solve questions related to Heap priority_queue will be used in c++, it is of two types ascending priority queue and descending priority queue.
To create a min heap the syntax is -
- priority_queue<int,vector<int>,greater<int>> pq;
To create a max heap the syntax is -
- priority_queue<int> pq;
priority_queue functions -
size() - returns the size of the queue
push() - pushes an element inside the queue
pop() - deletes the first element of the queue
empty() - checks whether the queue is empty or not
top() - returns a topmost element of the queue
Heap Interview Questions -
A resource to get in-depth knowledge -
Congrats! you have learned the fundamentals of Heap Data-Structure, make sure to subscribe to my blog to follow this series and follow me on Hashnode, where I'll be uploading content on Data Structures and Algorithms every weekend.