Learn To Think Recursively and Solve Recursion Problems in an Interview in 4 Steps

What is Recursion?

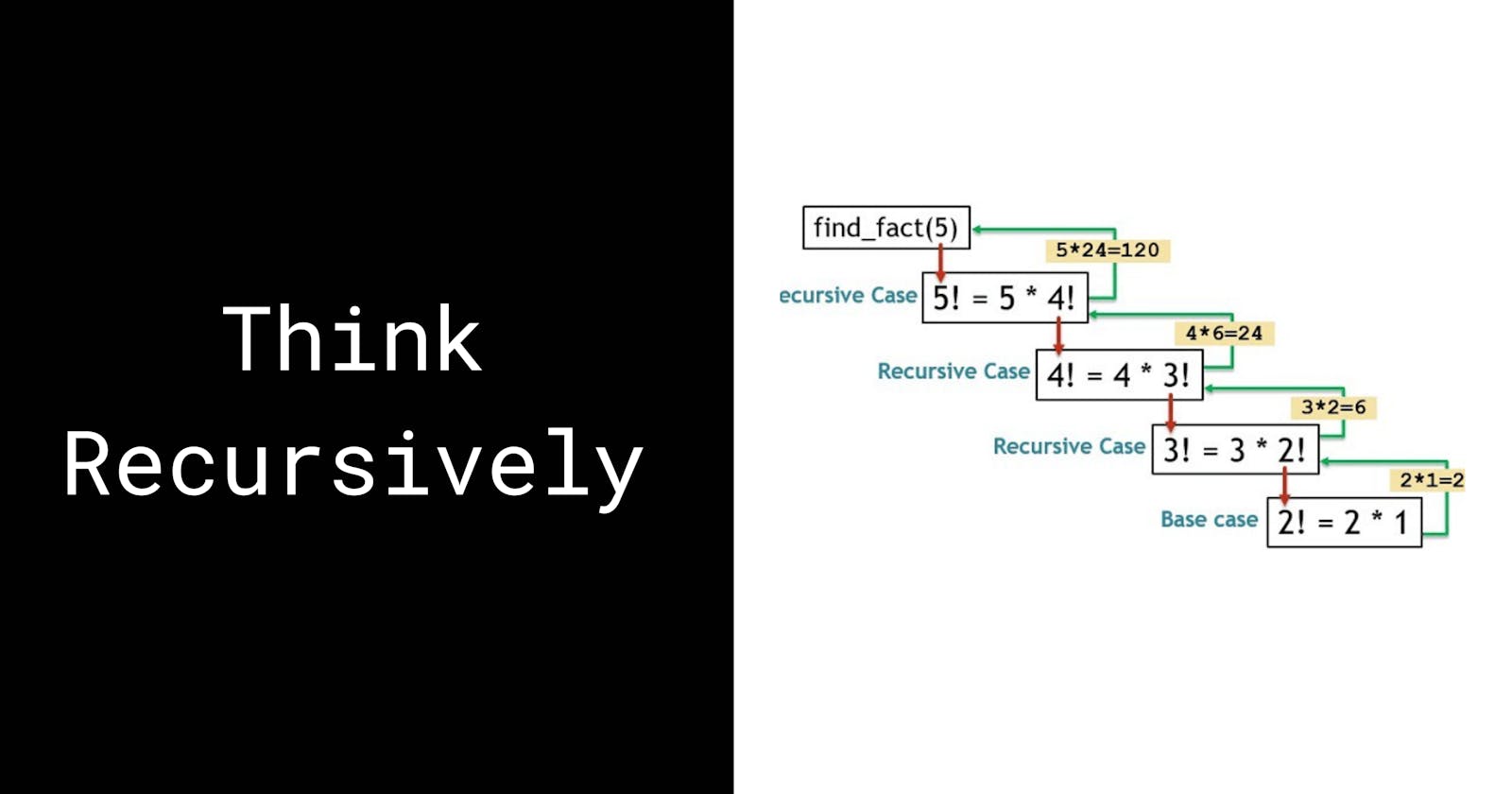
The process in which a function calls itself either directly or indirectly is called recursion and the corresponding function is called a recursive function with recursion you can solve some complex problems quite easily examples of such problems are tower of hanoi, tree traversals, DFS of graph etc.

properties of recursion -

performing the same operation multiple times with different inputs
At every step, the input is reduced to make the problem smaller
A base condition is required to stop the recursion process otherwise infinite loop will occur

Many people when try to solve a problem using recursion they try to trace each recursive call to determine what each function call is doing but this is a trap of endless confusion to avoid this trap you need not need to know what each function call is doing rather you just need to pick a subproblem and believe that your function will solve the rest of the problem, you need to take a leap of faith and believe in your function.

Steps to approach a problem and think recursively

Step 1) Know what your function is supposed to do.
Step 2) Determine a subproblem from the main problem.
Step 3) Find out the answer to the subproblem and use it to solve the main problem.
Step 4) Last step is to determine the base condition of the problem

Let's take a simple problem such as finding the sum of 1 to n numbers and follow the 4 steps mentioned above to solve the problem.

Know what your function is supposed to do

This is the most basic and general step but a very important one. Now in the question above, we know that we need to calculate the sum of numbers from 1 to n

So our function needs to take a value n and return the sum from 1 up to n so our inputs of the function cant exceed n.

let's say the function is sumTo().

int sumTo(int n){

}

Determine the subproblem from the main problem

A subproblem is any problem that is smaller than the main problem and it is important to find the appropriate subproblem

In the above case, the subproblem can be solving the sum of all numbers less than n.

so the appropriate subproblem will be solving for the sum of (n-1) numbers.

Finding out the answer to the subproblem and using it to solve the main problem

The solution for the sum of n-1 numbers will be

sumToSubProblem = 1+2+3 ...... + n-1

Now to find the solution to the main problem we just need to add the nth number -

mainProblem = subProblem + n

So the code will be

int sumTo(int n){
     int subProblem = sumTo(n-1);
     return subProblem + n;
}

The last step is to find the base case for the recursion process -

A base case condition is any condition that stops the recursion process and is necessary to avoid the infinite loop.

So to find the base condition we need to find at what input the function becomes irrelevant in the above case we know if n = 0 the function will become irrelevant as 0+0 will give 0 only.

so on applying this base condition we will have a complete solution to the main problem

int sumTo(n-1){
    if(n == 0) return 0;
    int subProblem = sumTo(n-1);
    return subProblem + n;
}

More examples -

Reversing a string using recursion

As per the first step, we know that we need a function that takes a string as input and return a reversed string.

string reverseString(string s){

}

Now we need to determine a subproblem which in this case will be leaving the first character and solving for the rest of the characters.

ie - string s = "hello";

so the subproblem will be reversing "ello" to "olle" and adding the first character 'h' in the end.

string reverseString(string s){
     string substring = s.substr(1,s.length());
     string reversedSubProblem = reverseString(substring);
     return reversedSubProblem + s[0];
}

Now the last step will be finding the base case condition which in this case will be if string s become empty string because that is the most basic string a user can provide.

so,

string reverseString(string s){
     if(s == "") return "";
     string substring = s.substr(1,s.length());
     string reversedSubProblem = reverseString(substring);
     return reversedSubProblem + s[0];
}

Similarly to find the nth Fibonacci number the subproblems will be finding the Fibonacci terms (n-1) and (n-2) and the addition of these two terms will give the solution for the nth Fibonacci term.

and the base condition, in this case, will be for n = 0 and n = 1 as there are no two previous terms for these values

int fibonacci(int n){
    if(n == 0) return 0;
    if(n == 1) return 1;
    int term1 = fibonacci(n-1);
    int term2 = fibonacci(n-2);
    return term1+term2;
}